Output from KPP

This chapter describes the source code files that are generated by KPP.

The Fortran90 code

The code generated by KPP is organized in a set of separate files. Each has a complete description of how it was generated at the begining of the file. The files associated with root are named with a corresponding prefix ROOT_ A short description of each file is contained in the following sections.

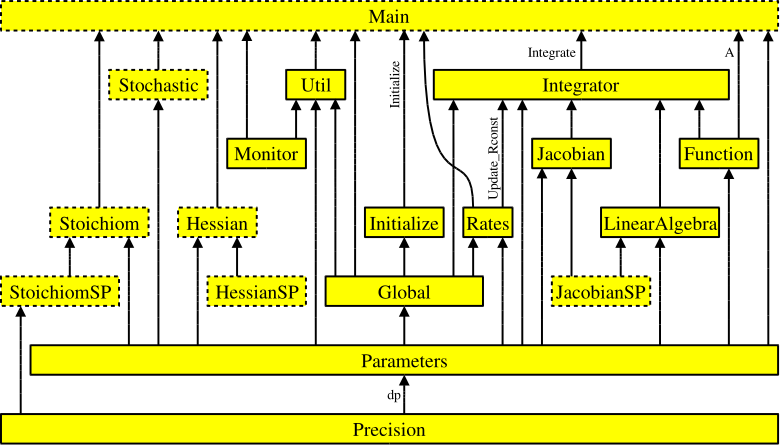
Figure 1: Interdependencies of the KPP-generated files. Each arrow starts at the module that exports a variable or subroutine and points to the module that imports it via the Fortran90 USE instruction. The prefix ROOT_ has been omitted from module names for better readability. Dotted boxes show optional files that are only produced under certain circumstances.

All subroutines and functions, global parameters, variables, and sparsity data structures are encapsulated in modules. There is exactly one module in each file, and the name of the module is identical to the file name but without the suffix .f90 or .F90. Figure 1 (above) shows how these modules are related to each other. The generated code is consistent with the Fortran90 standard. It may, however, exceed the official maximum number of 39 continuation lines.

Tip

The default Fortran90 file suffix is .f90. To have KPP generate Fortran90 code ending in .F90 instead, add the command #UPPERCASEF90 ON to the KPP definition file.

ROOT_Main

ROOT_Main.f90 (or .F90) root is the main Fortran90 program. It contains the driver after modifications by the substitution preprocessor. The name of the file is computed by KPP by appending the suffix to the root name.

Using #DRIVER none will skip generating this file.

ROOT_Model

The file ROOT_Model.f90 (or .F90) unifies all model definitions in a single module. This simplifies inclusion into external Fortran programs.

ROOT_Initialize

The file ROOT_Initialize.f90 (or .F9O) contains the subroutine Initialize, which defines initial values of the chemical species. The driver calls the subroutine once before the time integration loop starts.

ROOT_Integrator

The file ROOT_Integrator.f90 (or .F90) contains the subroutine Integrate, which is called every time step during the integration. The integrator that was chosen with the #INTEGRATOR command is also included in this file. In case of an unsuccessful integration, the module root provides a short error message in the public variable IERR_NAME.

ROOT_Monitor

The file ROOT_Monitor.f90 (.F90) contains arrays with information about the chemical mechanism. The names of all species are included in SPC_NAMES and the names of all equations are included in EQN_NAMES.

It was shown (cf. #EQNTAGS) that each reaction in the section may start with an equation tag which is enclosed in angle brackets, e.g.:

<R1> NO2 + hv = NO + O3P :  6.69e-1*(SUN/60.0e0);

If the equation tags are switched on, KPP also generates the PARAMETER array EQN_TAGS. In combination with EQN_NAMES and the function tag2num that converts the equation tag to the KPP-internal tag number, this can be used to describe a reaction:

PRINT*, ’Reaction 1 is:’, EQN_NAMES( tag2num( ’R1’ ) )

ROOT_Precision

Fortran90 code uses parameterized real types. ROOT_Precision.f90 (or .F90) contains the following real kind definitions:

! KPP_SP - Single precision kind
  INTEGER, PARAMETER :: &
    SP = SELECTED_REAL_KIND(6,30)
! KPP_DP - Double precision kind
  INTEGER, PARAMETER :: &
    DP = SELECTED_REAL_KIND(12,300)

Depending on the choice of the #DOUBLE command, the real variables are of type double (REAL(kind=dp)) or single precision (REAL(kind=sp)). Changing the parameters of the SELECTED_REAL_KIND function in this module will cause a change in the working precision for the whole model.

ROOT_Rates

The code to update the rate constants is in ROOT_Rates.f90 (or .F90). The user defined rate law functions (cf. Fortran90 subrotutines in ROOT_Rates) are also placed here.

Fortran90 subrotutines in ROOT_Rates

Function	Description
Update_PHOTO	Update photolysis rate coefficients
Update_RCONST	Update all rate coefficients
Update_SUN	Update sun intensity

ROOT_Parameters

Global parameters are defined and initialized in ROOT_Parameters.f90 (or .F90):

Parameters Declared in ROOT_Parameters

Parameter	Represents	Example
NSPEC	No. chemical species (NVAR + NFIX)	7
NVAR	No. variable species	5
NFIX	No. fixed species	2
NREACT	No. reactions	10
NONZERO	No. nonzero entries Jacobian	18
LU_NONZERO	As above, after LU factorization	19
NHESS	Length, sparse Hessian	10
NJVRP	Length, sparse Jacobian JVRP	13
NSTOICM	Length, stoichiometric matrix	22
ind_spc	Index of species spc in C
indf_spc	Index of fixed species spc in FIX

Example values listed in the 3rd column are taken from the small_strato mechanism (cf. Running KPP with an example stratospheric mechanism).

KPP orders the variable species such that the sparsity pattern of the Jacobian is maintained after an LU decomposition. For our example there are five variable species (NVAR = 5) ordered as

ind_O1D=1, ind_O=2, ind_O3=3, ind_NO=4, ind_NO2=5

and two fixed species (NFIX = 2)

ind_M = 6, ind_O2 = 7.

KPP defines a complete set of simulation parameters, including the numbers of variable and fixed species, the number of chemical reactions, the number of nonzero entries in the sparse Jacobian and in the sparse Hessian, etc.

ROOT_Global

Several global variables are declared in ROOT_Global.f90 (or .F90):

Global Variables Declared in ROOT_Global

Global variable	Represents
C(NSPEC)	Concentrations, all species
VAR(:)	Concentrations, variable species (pointer)
FIX(:)	Concentrations, fixed species (pointer)
RCONST(NREACT)	Rate coefficient values
TIME	Current integration time
SUN	Sun intensity between 0 and 1
TEMP	Temperature
TSTART, TEND	Simulation start/end time
DT	Simulation time step
ATOL(NSPEC)	Absolute tolerances
RTOL(NSPEC)	Relative tolerances
STEPMIN	Lower bound for time step
STEPMAX	Upper bound for time step
CFACTOR	Conversion factor

Both variable and fixed species are stored in the one-dimensional array C. The first part (indices from 1 to NVAR) contains the variable species, and the second part (indices from to NVAR+1 to NSPEC) the fixed species. The total number of species is the sum of the NVAR and NFIX. The parts can also be accessed separately through pointer variables VAR and FIX, which point to the proper elements in C.

VAR(1:NVAR) => C(1:NVAR)
FIX(1:NFIX) => C(NVAR+1:NSPEC)

Important

In previous versions of KPP, Fortran90 code was generated with VAR and FIX being linked to the C array with an EQUIVALENCE statement. This construction, however, is not thread-safe, and it prevents KPP-generated Fortran90 code from being used within parallel environments (e.g. such as an OpenMP parallel loop).

We have modified KPP 2.5.0 and later versions to make KPP-generated Fortran90 code thread-safe. VAR and FIX are now POINTER variables that point to the proper slices of the C array. They are also nullified when no longer needed. VAR and FIX are now also kept internal to the various integrator files located in the $KPP_HOME/int directory.

ROOT_Function

The chemical ODE system for our small_strato example (described in Running KPP with an example stratospheric mechanism) is:

\[\begin{split}\begin{aligned} \frac{d[O(^1D)]}{dt} & = & k_{5}\, [O_3] - k_{6}\, [O(^1D)]\, [M] - k_{7}\, [O(^1D)]\, [O_3]\\ \frac{d[O]}{dt} & = & 2\, k_{1}\, [O_2] - k_{2}\, [O]\, [O_2] + k_{3}\, [O_3]\\ & & - k_{4}\, [O]\, [O_3]+ k_{6}\, [O(^1D)]\, [M]\\ & & - k_{9}\, [O]\, [NO_2] + k_{10}\, [NO_2]\\ \frac{d[O_3]}{dt} & = & k_{2}\, [O]\, [O_2] - k_{3}\, [O_3] - k_{4}\, [O]\, [O_3] - k_{5}\, [O_3]\\ & & - k_{7}\, [O(^1D)]\, [O_3] - k_{8}\, [O_3]\, [NO]\\ \frac{d[NO]}{dt} & = & - k_{8}\, [O_3]\, [NO] + k_{9}\, [O]\, [NO_2] + k_{10}\, [NO_2]\\ \frac{d[NO_2]}{dt} & = & k_{8}\, [O_3]\, [NO] - k_{9}\, [O]\, [NO_2] - k_{10}\, [NO_2]\\ \end{aligned}\end{split}\]

where square brackets denote concentrations of the species. The code for the ODE function is in ROOT_Function.f90 (or .F90) The chemical reaction mechanism represents a set of ordinary differential equations (ODEs) of dimension . The concentrations of fixed species are parameters in the derivative function. The subroutine computes first the vector A of reaction rates and then the vector Vdot of variable species time derivatives. The input arguments V, F, RCT are the concentrations of variable species, fixed species, and the rate coefficients, respectively. A and Vdot may be returned to the calling program (for diagnostic purposes) with optional ouptut argument Aout. Below is the Fortran90 code generated by KPP for the ODE function of our small_strato example.

SUBROUTINE Fun (V, F, RCT, Vdot, Aout, Vdotout )

! V - Concentrations of variable species (local)
  REAL(kind=dp) :: V(NVAR)
! F - Concentrations of fixed species (local)
  REAL(kind=dp) :: F(NVAR)
! RCT - Rate constants (local)
  REAL(kind=dp) :: RCT(NREACT)
! Vdot - Time derivative of variable species concentrations
  REAL(kind=dp) :: Vdot(NVAR)
! Aout - Optional argument to return equation rate constants
  REAL(kind=dp), OPTIONAL :: Aout(NREACT)


! Computation of equation rates
  A(1) = RCT(1)*F(2)
  A(2) = RCT(2)*V(2)*F(2)
  A(3) = RCT(3)*V(3)
  A(4) = RCT(4)*V(2)*V(3)
  A(5) = RCT(5)*V(3)
  A(6) = RCT(6)*V(1)*F(1)
  A(7) = RCT(7)*V(1)*V(3)
  A(8) = RCT(8)*V(3)*V(4)
  A(9) = RCT(9)*V(2)*V(5)
  A(10) = RCT(10)*V(5)

  !### Use Aout to return equation rates
  IF ( PRESENT( Aout ) ) Aout = A

! Aggregate function
  Vdot(1) = A(5)-A(6)-A(7)
  Vdot(2) = 2*A(1)-A(2)+A(3) &
            -A(4)+A(6)-A(9)+A(10)
  Vdot(3) = A(2)-A(3)-A(4)-A(5) &
            -A(7)-A(8)
  Vdot(4) = -A(8)+A(9)+A(10)
  Vdot(5) = A(8)-A(9)-A(10)

END SUBROUTINE Fun

ROOT_Jacobian and ROOT_JacobianSP

The Jacobian matrix for our example contains 18 non-zero elements:

\[\begin{split}\begin{aligned} \mathbf{J}(1,1) & = & - k_{6}\, [{M}] - k_{7}\, [{O_3}]\\ \mathbf{J}(1,3) & = & k_{5} - k_{7}\, [{O(^1D)}]\\ \mathbf{J}(2,1) & = & k_{6}\, [{M}]\\ \mathbf{J}(2,2) & = & - k_{2}\, [{O_2}] - k_{4}\, [{O_3}] - k_{9}\, [{NO_2}]\\ \mathbf{J}(2,3) & = & k_{3} - k_{4}\, [{O}]\\ \mathbf{J}(2,5) & = & - k_{9}\, [{O}] + k_{10}\\ \mathbf{J}(3,1) & = & - k_{7}\, [{O_3}]\\ \mathbf{J}(3,2) & = & k_{2}\, [{O_2}] - k_{4}\, [{O_3}]\\ \mathbf{J}(3,3) & = & - k_{3} - k_{4}\, [{O}] - k_{5} - k_{7}\, [{O(^1D)}] - k_{8}\, [{NO}]\\ \mathbf{J}(3,4) & = & - k_{8}\, [{O_3}]\\ \mathbf{J}(4,2) & = & k_{9}\, [{NO_2}]\\ \mathbf{J}(4,3) & = & - k_{8}\, [{NO}]\\ \mathbf{J}(4,4) & = & - k_{8}\, [{O_3}]\\ \mathbf{J}(4,5) & = & k_{9}\, [{O}] + k_{10}\\ \mathbf{J}(5,2) & = & - k_{9}\, [{NO_2}]\\ \mathbf{J}(5,3) & = & k_{8}\, [{NO}]\\ \mathbf{J}(5,4) & = & k_{8}\, [{O_3}]\\ \mathbf{J}(5,5) & = & - k_{9}\, [{O}] - k_{10}\\ \end{aligned}\end{split}\]

It defines how the temporal change of each chemical species depends on all other species. For example, \(\mathbf{J}(5,2)\) shows that \(NO_2\) (species number 5) is affected by \(O\) (species number 2) via reaction R9. The sparse data structures for the Jacobian are declared and initialized in ROOT_JacobianSP.f90 (or .F90). The code for the ODE Jacobian and sparse multiplications is in ROOT_Jacobian.f90 (or .F90).

Tip

Adding either #JACOBIAN SPARSE_ROW or #JACOBIAN SPARSE_LU_ROW to the KPP definition file will create the file ROOT_JacobianSP.f90 (or .F90).

The Jacobian of the ODE function is automatically constructed by KPP. KPP generates the Jacobian subroutine Jac or JacSP where the latter is generated when the sparse format is required. Using the variable species V, the fixed species F, and the rate coefficients RCT as input, the subroutine calculates the Jacobian JVS. The default data structures for the sparse compressed on rows Jacobian representation (for the case where the LU fill-in is accounted for) are:

Sparse Jacobian Data Structures

Global variable	Represents
JVS(LU_NONZERO)	Jacobian nonzero elements
LU_IROW(LU_NONZERO)	Row indices
LU_ICOL(LU_NONZERO)	Column indices
LU_CROW(NVAR+1)	Start of rows
LU_DIAG(NVAR+1)	Diagonal entries

JVS stores the LU_NONZERO elements of the Jacobian in row order. Each row I starts at position LU_CROW(I), and LU_CROW(NVAR+1) = LU_NONZERO+1. The location of the I-th diagonal element is LU_DIAG(I). The sparse element JVS(K) is the Jacobian entry in row LU_IROW(K) and column LU_ICOL(K). For the small_strato example KPP generates the following Jacobian sparse data structure:

LU_ICOL = (/ 1,3,1,2,3,5,1,2,3,4, &
            5,2,3,4,5,2,3,4,5 /)
LU_IROW = (/ 1,1,2,2,2,2,3,3,3,3, &
            3,4,4,4,4,5,5,5,5 /)
LU_CROW = (/ 1,3,7,12,16,20 /)
LU_DIAG = (/ 1,4,9,14,19,20 /)

This is visualized in Figure 2 below.. The sparsity coordinate vectors are computed by KPP and initialized statically. These vectors are constant as the sparsity pattern of the Jacobian does not change during the computation.

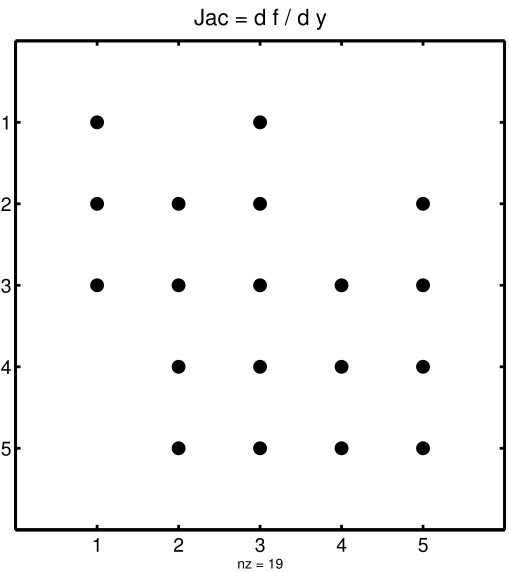
Figure 2: The sparsity pattern of the Jacobian for the small_strato example. All non-zero elements are marked with a bullet. Note that even though \(\mathbf{J}(3,5)\) is zero, it is also included here because of the fill-in.

Two other KPP-generated routines, Jac_SP_Vec and JacTR_SP_Vec (see Fortran90 subroutines in ROOT_Jacobian) are useful for direct and adjoint sensitivity analysis. They perform sparse multiplication of JVS (or its transpose for JacTR_SP_Vec) with the user-supplied vector UV without any indirect addressing.

Fortran90 subroutines in ROOT_Jacobian

Function	Description
Jac_SP	ODE Jacobian in sparse format
Jac_SP_Vec	Sparse multiplication
JacTR_SP_Vec	Sparse multiplication
Jac	ODE Jacobian in full format

ROOT_Hessian and ROOT_HessianSP

The sparse data structures for the Hessian are declared and initialized in ROOT_Hessian.f90 (or .F90). The Hessian function and associated sparse multiplications are in ROOT_HessianSP.f90 (or .F90).

The Hessian contains the second order derivatives of the time derivative functions. More exactly, the Hessian is a 3-tensor such that

\[H_{i,j,k} = \frac{\partial^2 ({\mathrm{d}}c/{\mathrm{d}}t)_i}{\partial c_j \,\partial c_k}~, \qquad 1 \le i,j,k \le N_{\rm var}~. \label{eqn:Hessian1}\]

KPP generates the routine Hessian:

Fortran90 functions in ROOT_Hessian

Function	Description
Hessian	ODE Hessian in sparse format
Hess_Vec	Hessian action on vectors
HessTR_Vec	Transposed Hessian action on vectors

Using the variable species V, the fixed species F, and the rate coefficients RCT as input, the subroutine Hessian calculates the Hessian. The Hessian is a very sparse tensor. The sparsity of the Hessian for our example is visualized in Figure 3: The Hessian of the small_strato example.

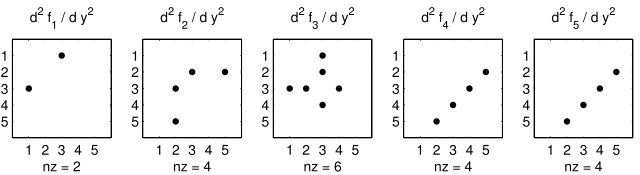
Figure 3: The Hessian of the small_strato example.

KPP computes the number of nonzero Hessian entries and saves it in the variable NHESS. The Hessian itself is represented in coordinate sparse format. The real vector HESS holds the values, and the integer vectors IHESS_I, IHESS_J, and IHESS_K hold the indices of nonzero entries as illustrated in Sparse Hessian Data.

Sparse Hessian Data

Variable	Represents
HESS(NHESS)	Hessian nonzero elements \(H_{i,j,k}\)
IHESS_I(NHESS)	Index \(i\) of element \(H_{i,j,k}\)
IHESS_J(NHESS)	Index \(j\) of element \(H_{i,j,k}\)
IHESS_J(NHESS)	Index \(k\) of element \(H_{i,j,k}\)

Since the time derivative function is smooth, these Hessian matrices are symmetric, \(\tt HESS_{i,j,k}\)=\(\tt HESS_{i,k,j}\). KPP stores only those entries \(\tt HESS_{i,j,k}\) with \(j \le k\). The sparsity coordinate vectors IHESS_1, IHESS_J and IHESS_K are computed by KPP and initialized statically. They are constant as the sparsity pattern of the Hessian does not change during the computation.

The routines Hess_Vec and HessTR_Vec compute the action of the Hessian (or its transpose) on a pair of user-supplied vectors U1 and U2. Sparse operations are employed to produce the result vector.

ROOT_LinearAlgebra

Sparse linear algebra routines are in the file ROOT_LinearAlgebra.f90 (or .F90). To numerically solve for the chemical concentrations one must employ an implicit timestepping technique, as the system is usually stiff. Implicit integrators solve systems of the form

\[P\, x = (I - h \gamma J)\, x = b\]

where the matrix \(P=I - h \gamma J\) is refered to as the “prediction matrix”. \(I\) the identity matrix, \(h\) the integration time step, \(\gamma\) a scalar parameter depending on the method, and \(J\) the system Jacobian. The vector \(b\) is the system right hand side and the solution \(x\) typically represents an increment to update the solution.

The chemical Jacobians are typically sparse, i.e. only a relatively small number of entries are nonzero. The sparsity structure of \(P\) is given by the sparsity structure of the Jacobian, and is produced by KPP (with account for the fill-in) as discussed above.

KPP generates the sparse linear algebra subroutine KppDecomp (see Fortran90 functions in ROOT_LinearAlgebra) which performs an in-place, non-pivoting, sparse LU decomposition of the prediction matrix \(P\). Since the sparsity structure accounts for fill-in, all elements of the full LU decomposition are actually stored. The output argument IER returns a value that is nonzero if singularity is detected.

Fortran90 functions in ROOT_LinearAlgebra

Function	Description
KppDecomp	Sparse LU decomposition
KppSolve	Sparse back subsitution
KppSolveTR	Transposed sparse back substitution

The subroutines KppSolve and KppSolveTr and use the in-place LU factorization \(P\) as computed by and perform sparse backward and forward substitutions (using \(P\) or its transpose). The sparse linear algebra routines KppDecomp and KppSolve are extremely efficient, as shown by Sandu et al. [1996].

ROOT_Stoichiom and ROOT_StoichiomSP

These files contain contain a description of the chemical mechanism in stoichiometric form. The file ROOT_Stoichiom.f90 (or .F90) contains the functions for reactant products and its Jacobian, and derivatives with respect to rate coefficients. The declaration and initialization of the stoichiometric matrix and the associated sparse data structures is done in ROOT_StochiomSP.f90 (or .F90).

Tip

Adding #STOICMAT ON to the KPP definition file will create the file ROOT_Stoichiom.f90 (or .F90) Also, if either #JACOBIAN SPARSE ROW or #JACOBIAN SPARSE_LU_ROW are also added to the KPP definition file, the file ROOT_StoichiomSP.f90 (or .F90) will also be created.

The stoichiometric matrix is constant sparse. For our example the matrix NSTOICM=22 has 22 nonzero entries out of 50 entries. KPP produces the stoichiometric matrix in sparse, column-compressed format, as shown in Sparse Stoichiometric Matrix. Elements are stored in columnwise order in the one-dimensional vector of values STOICM. Their row and column indices are stored in ICOL_STOICM and ICOL_STOICM respectively. The vector CCOL_STOICM contains pointers to the start of each column. For example column j starts in the sparse vector at position CCOL_STOICM(j) and ends at CCOL_STOICM(j+1)-1. The last value CCOL_STOICM(NVAR) = NSTOICHM+1 simplifies the handling of sparse data structures.

Sparse Stoichiometric Matrix

Variable	Represents
STOICM(NSTOICM)	Stoichiometric matrix
IROW_STOICM(NSTOICM)	Row indices
ICOL_STOICM(NSTOICM)	Column indices
CCOL_STOICM(NREACT+1)	Start of columns

Fortran90 functions in ROOT_Stoichiom

Variable	Represents
dFun_dRcoeff	Derivatives of Fun w/r/t rate coefficients
dJac_dRcoeff	Derivatives of Jac w/r/t rate coefficients
ReactantProd	Reactant products
JacReactantProd	Jacobian of reactant products

The subroutine ReactantProd (see Fortran90 functions in ROOT_Stoichiom) computes the reactant products ARP for each reaction, and the subroutine JacReactantProd computes the Jacobian of reactant products vector, i.e.:

\[\begin{aligned} \tt JVRP = {\partial{\tt ARP}}/{\partial{\tt V}} \end{aligned}\]

The matrix JVRP is sparse and is computed and stored in row compressed sparse format, as shown in Fortran90 functions in ROOT_Hessian. The parameter NJVRP holds the number of nonzero elements. For our small_strato example:

NJVRP = 13
CROW_JVRP = (/ 1,1,2,3,5,6,7,9,11,13,14 /)
ICOL_JVRP = (/ 2,3,2,3,3,1,1,3,3,4,2,5,4 /)

Sparse Data for Jacobian of Reactant Products

Variable	Represents
JVRP(NJVRP)	Nonzero elements of JVRP
ICOL_JVRP(NJVRP)	Column indices of JVRP
IROW_JVRP(NJVRP)	Row indices of JVRP
CROW_JVRP(NREACT+1)	Start of rows in JVRP

If #STOICMAT is set to ON, the stoichiometric formulation allows a direct computation of the derivatives with respect to rate coefficients.

The subroutine dFun_dRcoeff computes the partial derivative DFDR of the ODE function with respect to a subset of NCOEFF reaction coefficients, whose indices are specified in the array

\[\begin{aligned} \tt DFDR = {\partial{\tt Vdot}}/{\partial{\tt RCT(JCOEFF)}} \end{aligned}\]

Similarly one can obtain the partial derivative of the Jacobian with respect to a subset of the rate coefficients. More exactly, KPP generates the subroutine dJacR_dCoeff, which calculates DJDR, the product of this partial derivative with a user-supplied vector U:

\[\begin{aligned} \tt DJDR = [{\partial{\tt JVS}}/{\partial{\tt RCT(JCOEFF)}}] \times {\tt U} \end{aligned}\]

ROOT_Stochastic

If the generation of stochastic functions is switched on (i.e. when the command #STOCHASTIC ON is added to the KPP definition file), KPP produces the file ROOT_Stochastic.f90 (or .F90), with the following functions:

Propensity calculates the propensity vector. The propensity function uses the number of molecules of variable (Nmlcv) and fixed (Nmlcf) species, as well as the stochastic rate coefficients (SCT) to calculate the vector of propensity rates (Propensity). The propensity \(\tt Prop_j\) defines the probability that the next reaction in the system is the \(j^{th}\) reaction.

StochasticRates converts deterministic rates to stochastic. The stochastic rate coefficients (SCT) are obtained through a scaling of the deterministic rate coefficients (RCT). The scaling depends on the Volume of the reaction container and on the number of molecules which react.

MoleculeChange calculates changes in the number of molecules. When the reaction with index IRCT takes place, the number of molecules of species involved in that reaction changes. The total number of molecules is updated by the function.

These functions are used by the Gillespie numerical integrators (direct stochastic simulation algorithm). These integrators are provided in both Fortran90 and C implementations (the template file name is gillespie). Drivers for stochastic simulations are also implemented (the template file name is general_stochastic.).

ROOT_Util

In addition to the chemical system description routines discussed above, KPP generates several utility subroutines and functions in the file ROOT_Util.f90 (or .F90).

Fortran90 subroutines and functions in ROOT_Util

Function	Description
GetMass	Check mass balance for selected atoms
Shuffle_kpp2user	Shuffle concentration vector
Shuffle_user2kpp	Shuffle concentration vector
InitSaveData	Utility for #LOOKAT command
SaveData	Utility for #LOOKAT command
CloseSaveData	Utility for #LOOKAT command
tag2num	Calculate reaction number from equation tag
Integrator_Update_Options	Choose Update_RCONST/PHOTO/SUN

The subroutines InitSaveData, SaveData, and CloseSaveData can be used to print the concentration of the species that were selected with #LOOKAT to the file ROOT.dat (cf. #LOOKAT and #MONITOR).

ROOT_mex_Fun, ROOT_mex_Jac_SP, and ROOT_mex_Hessian

Mex is a Matlab extension. KPP generates the mex routines for the ODE function, Jacobian, and Hessian, for the target languages C, Fortran77, and Fortran90.

Tip

To generate Mex files, add the command #MEX ON to the KPP definition file.

After compilation (using Matlab’s mex compiler) the mex functions can be called instead of the corresponding Matlab m-functions. Since the calling syntaxes are identical, the user only has to insert the mex string within the corresponding function name. Replacing m-functions by mex-functions gives the same numerical results, but the computational time could be considerably smaller, especially for large kinetic systems.

If possible we recommend to build mex files using the C language, as Matlab offers most mex interface options for the C language. Moreover, Matlab distributions come with a native C compiler (lcc) for building executable functions from mex files. The mex files built using Fortran90 may require further platform-specific tuning of the mex compiler options.

The C code

Important

Some run-time options for C-language integrators (specified in the ICNTRL and RCNTRL arrays) do not exactly correspond to the Fortran90 run-time options. We will standardize run-time integrator options across all target languages in a future KPP release.

The driver file ROOT.c contains the main (driver) program and numerical integrator functions, as well as declarations and initializations of global variables.

The generated C code includes three header files which are #include-d in other files as appropriate.

1. The global parameters (cf. Parameters Declared in ROOT_Parameters) are #include-d in the header file ROOT_Parameters.h

2. The global variables (cf. Global Variables Declared in ROOT_Global) are extern-declared in ROOT_Global.h and declared in the driver file ROOT.c.

3. The header file ROOT_Sparse.h contains extern declarations of sparse data structures for the Jacobian (cf. Sparse Jacobian Data Structures),Hessian (cf. Sparse Hessian Data) and stoichiometric matrix (cf. Sparse Stoichiometric Matrix), and the Jacobian of reaction products (cf. Sparse Data for Jacobian of Reactant Products). The actual declarations of each datastructures is done in the corresponding files.

The code for the ODE function (see section ROOT_Function) is in ROOT_Function.c. The code for the ODE Jacobian and sparse multiplications (cf. ROOT_Jacobian and ROOT_JacobianSP) is in ROOT_Jacobian.c, and the declaration and initialization of the Jacobian sparse data structures is in the file ROOT_JacobianSP.c. Similarly, the Hessian function and associated sparse multiplications (cf. ROOT_Hessian and ROOT_HessianSP) are in ROOT_Hessian.c, and the declaration and initialization of Hessian sparse data structures are in ROOT_HessianSP.c.

The file ROOT_Stoichiom.c contains the functions for reactant products and its Jacobian, and derivatives with respect to rate coefficients (cf. ROOT_Stoichiom and ROOT_StoichiomSP) . The declaration and initialization of the stoichiometric matrix and the associated sparse data structures (cf. Sparse Stoichiometric Matrix) is done in ROOT_StoichiomSP.c.

Sparse linear algebra routines (cf. ROOT_LinearAlgebra) are in the file ROOT_LinearAlgebra.c. The code to update the rate constants and user defined code for rate laws is in ROOT_Rates.c.

Various utility and input/output functions (cf. ROOT_Util) are in ROOT_Util.c and ROOT_Monitor.c.

Finally, mex gateway routines that allow the C implementation of the ODE function, Jacobian, and Hessian to be called directly from Matlab (cf. ROOT_mex_Fun, ROOT_mex_Jac_SP, and ROOT_mex_Hessian) are also generated (in the files ROOT_mex_Fun.c, ROOT_mex_Jac_SP.c, and ROOT_mex_Hessian.c).

The Matlab code

Important

Some run-time options for Matlab-language integrators (specified in the ICNTRL and RCNTRL arrays) do not exactly correspond to the Fortran90 run-time options. We will standardize run-time integrator options across all target languages in a future KPP release.

Matlab provides a high-level programming environment that allows algorithm development, numerical computations, and data analysis and visualization. The KPP-generated Matlab code allows for a rapid prototyping of chemical kinetic schemes, and for a convenient analysis and visualization of the results. Differences between different kinetic mechanisms can be easily understood. The Matlab code can be used to derive reference numerical solutions, which are then compared against the results obtained with user-supplied numerical techniques. KPP/Matlab can also be used to teach students fundamentals of chemical kinetics and chemical numerical simulations.

Each Matlab function has to reside in a separate m-file. Function calls use the m-function-file names to reference the function. Consequently, KPP generates one m-function-file for each of the functions discussed in the sections entitled ROOT_Function , ROOT_Jacobian and ROOT_JacobianSP, ROOT_Hessian and ROOT_HessianSP, ROOT_Stoichiom and ROOT_StoichiomSP, ROOT_Util. The names of the m-function-files are the same as the names of the functions (prefixed by the model name ROOT.

The variables of Parameters Declared in ROOT_Parameters are defined as Matlab global variables and initialized in the file ROOT_parameter_defs.m. The variables of Global Variables Declared in ROOT_Global are declared as Matlab global variables in the file ROOT_global_defs.m. They can be accessed from within each Matlab function by using declarations of the variables of interest.

The sparse data structures for the Jacobian (cf. Sparse Jacobian Data Structures), the Hessian (cf. Sparse Hessian Data), the stoichiometric matrix (cf. Sparse Stoichiometric Matrix), and the Jacobian of reaction (see Sparse Data for Jacobian of Reactant Products) are declared as Matlab global variables in the file ROOT_Sparse_defs.m. They are initialized in separate m-files, namely ROOT_JacobianSP.m, ROOT_HessianSP.m, and ROOT_StoichiomSP.m respectively.

Two wrappers (ROOT_Fun_Chem.m and ROOT_Jac_SP_Chem.m) are provided for interfacing the ODE function and the sparse ODE Jacobian with Matlab’s suite of ODE integrators. Specifically, the syntax of the wrapper calls matches the syntax required by Matlab’s integrators like ode15s. Moreover, the Jacobian wrapper converts the sparse KPP format into a Matlab sparse matrix.

List of Matlab model files

Function	Description
ROOT.m	Driver
ROOT_parameter_defs.m	Global parameters
ROOT_global_defs.m	Global variables
ROOT_sparse_defs.m	Global sparsity data
ROOT_Fun_Chem.m	Template for ODE function
ROOT_Fun.m	ODE function
ROOT_Jac_Chem.m	Template for ODE Jacobian
ROOT_Jac_SP.m	Jacobian in sparse format
ROOT_JacobianSP.m	Sparsity data structures
ROOT_Hessian.m	ODE Hessian in sparse format
ROOT_HessianSP.m	Sparsity data structures
ROOT_Hess_Vec.m	Hessian action on vectors
ROOT_HessTR_Vec.m	Transposed Hessian action on vectors
ROOT_stoichiom.m	Derivatives of Fun and Jac w/r/t rate coefficients
ROOT_stochiomSP.m	Sparse data
ROOT_ReactantProd.m	Reactant products
ROOT_JacReactantProd.m	Jacobian of reactant products
ROOT_Rates.m	User-defined rate reaction laws
ROOT_Update_PHOTO.m	Update photolysis rate coefficients
ROOT_Update_RCONST.m	Update all rate coefficients
ROOT_Update_SUN.m	Update sola intensity
ROOT_GetMass.m	Check mass balance for selected atoms
ROOT_Initialize.m	Set initial values
ROOT_Shuffle_kpp2user.m	Shuffle concentration vector
ROOT_Shuffle_user2kpp.m	Shuffle concentration vector

The Makefile

KPP produces a Makefile that allows for an easy compilation of all KPP-generated source files. The file name is Makefile_ROOT. The Makefile assumes that the selected driver contains the main program. However, if no driver was selected (i.e. #DRIVER none), it is necessary to add the name of the main program file manually to the Makefile.

The log file

The log file ROOT.log contains a summary of all the functions, subroutines and data structures defined in the code file, plus a summary of the numbering and category of the species involved.

This file contains supplementary information for the user. Several statistics are listed here, like the total number equations, the total number of species, the number of variable and fixed species. Each species from the chemical mechanism is then listed followed by its type and numbering.

Furthermore it contains the complete list of all the functions generated in the target source file. For each function, a brief description of the computation performed is attached containing also the meaning of the input and output parameters.

Output from the Integrators (ISTATUS and RSTATUS)

In order to obtain more information about the integration, KPP provides the arrays ISTATUS (integer) and RSTATUS (real). Each of them is an array of 20 elements. Array elements not listed here are currently not used. Details can be found in the comment lines of the individual integrator files in $KPP_HOME/int/.

ISTATUS

Summary of ISTATUS usage in the f90 integrators. Here, Y = used.

ISTATUS	1	2	3	4	5	6	7	8	9
beuler	Y	Y	Y	Y	Y	Y	Y	Y
dvode
exponential
feuler
gillespie
lsode	Y	Y	Y
radau5	Y	Y	Y	Y	Y	Y	Y	Y
rosenbrock_adj	Y	Y	Y	Y	Y	Y	Y	Y
rosenbrock	Y	Y	Y	Y	Y	Y	Y	Y
rosenbrock_tlm	Y	Y	Y	Y	Y	Y	Y	Y	Y
rosenbrock_autoreduce	Y	Y	Y	Y	Y	Y	Y	Y
runge_kutta_adj	Y	Y	Y	Y	Y	Y	Y	Y
runge_kutta	Y	Y	Y	Y	Y	Y	Y	Y
runge_kutta_tlm	Y	Y	Y	Y	Y	Y	Y	Y
sdirk4	Y	Y	Y	Y	Y	Y	Y	Y
sdirk_adj	Y	Y	Y	Y	Y	Y	Y	Y
sdirk	Y	Y	Y	Y	Y	Y	Y	Y
sdirk_tlm	Y	Y	Y	Y	Y	Y	Y	Y
seulex	Y	Y	Y	Y	Y	Y	Y
tau_leap

ISTATUS(1)

Number of function calls.

ISTATUS(2)

Number of Jacobian calls.

ISTATUS(3)

Number of steps.

ISTATUS(4)

Number of accepted steps.

ISTATUS(5)

Number of rejected steps (except at very beginning).

ISTATUS(6)

Number of LU decompositions.

ISTATUS(7)

Number of forward/backward substitutions.

ISTATUS(8)

Number of singular matrix decompositions.

ISTATUS(9)

Number of Hessian calls.

ISTATUS(10) ... ISTATUS(20)

Currently not used.

RSTATUS

Summary of RSTATUS usage in the f90 integrators. Here, Y = used, s = solver specific usage.

RSTATUS	1	2	3	4
beuler	Y	Y	Y
dvode
exponential
feuler
gillespie
lsode	Y	Y
radau5
rosenbrock_adj	Y	Y	Y
rosenbrock	Y	Y	Y
rosenbrock_tlm	Y	Y	Y
rosenbrock_autoreduce	Y	Y	Y	s
runge_kutta_adj	Y	Y	Y
runge_kutta	Y	Y	Y
runge_kutta_tlm	Y	Y	Y
sdirk4	Y	Y
sdirk_adj	Y	Y	Y
sdirk	Y	Y	Y
sdirk_tlm	Y	Y	Y
seulex
tau_leap

RSTATUS(1)

Texit, the time corresponding to the computed \(Y\) upon return.

RSTATUS(2)

Hexit: the last accepted step before exit.

RSTATUS(3)

Hnew: The last predicted step (not yet taken. For multiple restarts, use Hnew as Hstart in the subsequent run.

RSTATUS(4)

(Solver-specific for rosenbrock_autoreduce) AR_thr: used to output the calculated (used) auto-reduction threshold for the integration. Useful when ICNTRL(10) > 0 where the threshold is dynamically determined based on a given species.

RSTATUS(5) ... RSTATUS(20)

Currently not used.